Quantitative sociology and Economical Complexity: Statistical mechanics of decision makers
The idea of using Statistical Mechanics for modeling complexity inside societies made of human beings has been widely pointed us, as for instance by Daurlauf first, from a philosophycal perspective, and then -more concretely- by Brock and Daurlauf, that roughly re-discovered the Curie-Weiss behavior among decision makers [humans reduced to binary actions, a thing called "discrete choice" whose genesis has to be traced back in Econometrics and coupled to the original ideas of Daniel McFadden (Nobel Prize in Economics)]. While interactions have been first considered of imitative fashion only, thus with a strong simplification w.r.t. glassy behavior where competition is also present, resulting in frustration, the underlying network where decision makers interact has always been accounted and fully connected models play marginal role in this context. In particular, driven by the pioneering discoveries of Stanely Milgram on the so called "six degrees of separation", in 2003 Watts and Strogatz posed the basis of complex graph theory giving an explicit recipe for builiding "small world" networks, namely graphs with low diamater (growing logharitmical with the amount of nodes) and high clustering coefficient, whose properties are different from standard random graphs as those developed by the fathers of graph theory, Erdos and Renyi.
Thus, usually in modeling social dynamics we have to mix statistical mechanics and graph theory for pasting imitative (or competitive) interactions of agents -having the freedom of a discrete choice (i.e. a spin)- on a small world topology (or, sometimes -e.g. for the sexual relations- scale free topologies).
My research focuses on understanding how, due to globalization (that produced a never-saw-in-the-past mobility of travellers), migrants are integrated in a host society (from a sociological perspective) and how this affects the overall GDP of the host nation due to the consequent lowering of trade's costs among the origin and the host country, thus linking social perspectives with economical complexity.
In particular we consider two parties, the first made of by host citizens and the second made of by migrants (worldwide incoming) and agents belonging to these two parties may interact. The topology of this bipartite structure is simply random (a bipartite Erdos-Renyi model) because the randomness in the migrant's process is huge and correlations among migrants washes away averaging over the various countries of origin of migrants.
On this system we analyze different degrees of freedom (classical social quantifiers), as for instance the evolution of mixed marriages M (host/migrant) or the evolution of the labor market for migrants L. It is worth pointing out that, instead of approaching the problem with classical time series, hence studying M(t) or L(t), we collect also the percentage of migrants inside the host society -that we call Gamma- and, as Gamma(t) is monotonically increasing and, as we consider time windows of at least one (sometimes even two) decade -enough time to allow complete thermalization in the process of contracting marriages- we invert Gamma(t) -> t(Gamma) that we then use to past in M(t) and L(t), for obtaining M(Gamma) and L(Gamma).
If at the basis of the marriages, in agreement with Sociologist's theories, we assume mainly imitation, that is, if we say that the "most stable" configuration for a possible couple host/migrants are those where or both the migrant and the host are satisfied by the marriages (+,+), or both are satisfied being not marriages (-,-), and the conflictual configurations where the host wants to be married with the stranger but the stranger does not (+,-) and viceversa (-,+), we are just saying that we have to consider ferromagnetic interactions on this bipartite-random-network.
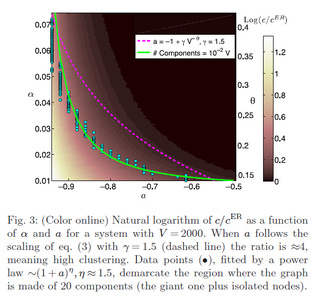
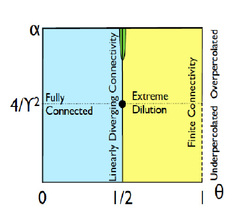
Remarkably, it is possible to show that such a structure is thermodynamically equivalent (shares the same partition function) to a network made of by citizens only, whose topological properties are however small world, thus giving a firm and novel ground to Milgram and Granovetter findings -a different route that brings the same results of Watts and Strogatz rewiring procedure.
Thus, usually in modeling social dynamics we have to mix statistical mechanics and graph theory for pasting imitative (or competitive) interactions of agents -having the freedom of a discrete choice (i.e. a spin)- on a small world topology (or, sometimes -e.g. for the sexual relations- scale free topologies).
My research focuses on understanding how, due to globalization (that produced a never-saw-in-the-past mobility of travellers), migrants are integrated in a host society (from a sociological perspective) and how this affects the overall GDP of the host nation due to the consequent lowering of trade's costs among the origin and the host country, thus linking social perspectives with economical complexity.
In particular we consider two parties, the first made of by host citizens and the second made of by migrants (worldwide incoming) and agents belonging to these two parties may interact. The topology of this bipartite structure is simply random (a bipartite Erdos-Renyi model) because the randomness in the migrant's process is huge and correlations among migrants washes away averaging over the various countries of origin of migrants.
On this system we analyze different degrees of freedom (classical social quantifiers), as for instance the evolution of mixed marriages M (host/migrant) or the evolution of the labor market for migrants L. It is worth pointing out that, instead of approaching the problem with classical time series, hence studying M(t) or L(t), we collect also the percentage of migrants inside the host society -that we call Gamma- and, as Gamma(t) is monotonically increasing and, as we consider time windows of at least one (sometimes even two) decade -enough time to allow complete thermalization in the process of contracting marriages- we invert Gamma(t) -> t(Gamma) that we then use to past in M(t) and L(t), for obtaining M(Gamma) and L(Gamma).
If at the basis of the marriages, in agreement with Sociologist's theories, we assume mainly imitation, that is, if we say that the "most stable" configuration for a possible couple host/migrants are those where or both the migrant and the host are satisfied by the marriages (+,+), or both are satisfied being not marriages (-,-), and the conflictual configurations where the host wants to be married with the stranger but the stranger does not (+,-) and viceversa (-,+), we are just saying that we have to consider ferromagnetic interactions on this bipartite-random-network.
Remarkably, it is possible to show that such a structure is thermodynamically equivalent (shares the same partition function) to a network made of by citizens only, whose topological properties are however small world, thus giving a firm and novel ground to Milgram and Granovetter findings -a different route that brings the same results of Watts and Strogatz rewiring procedure.
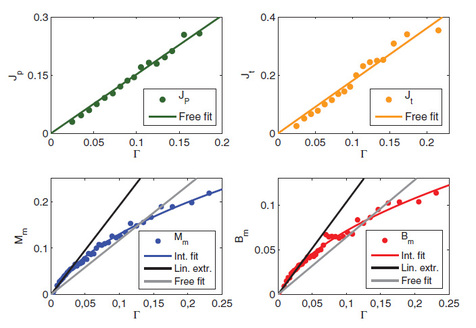
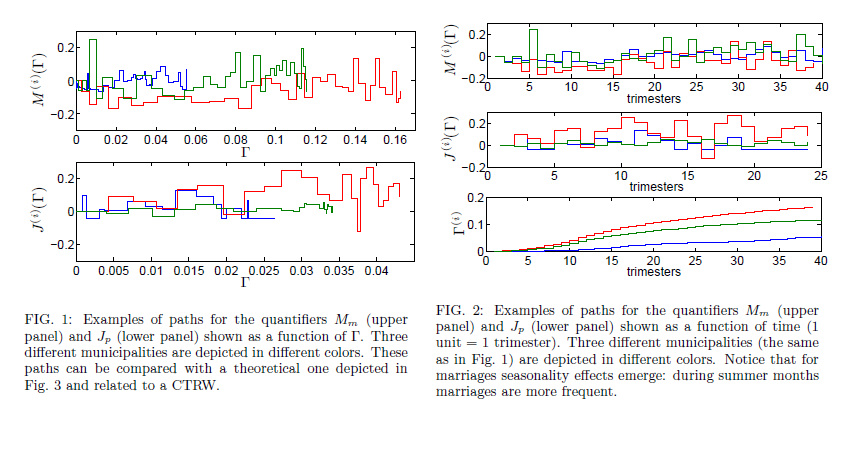
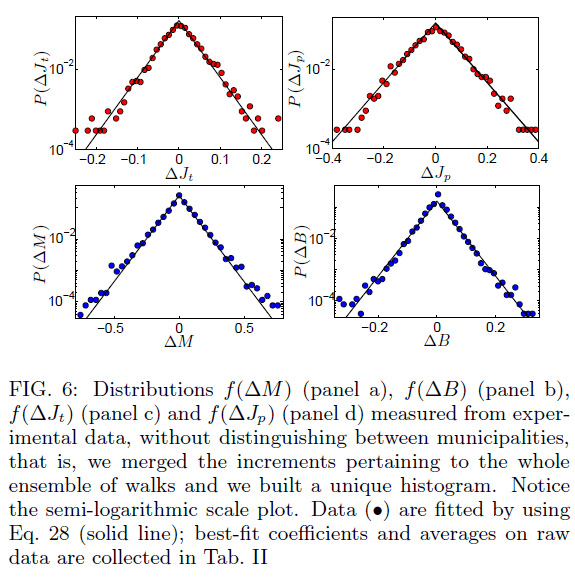
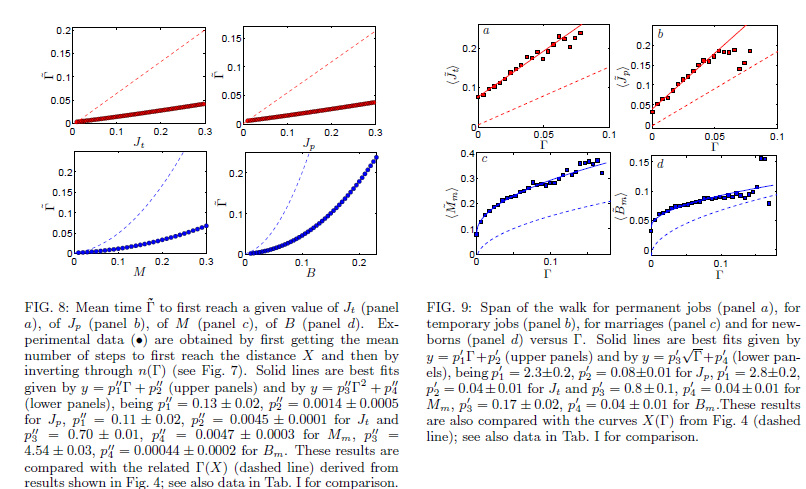
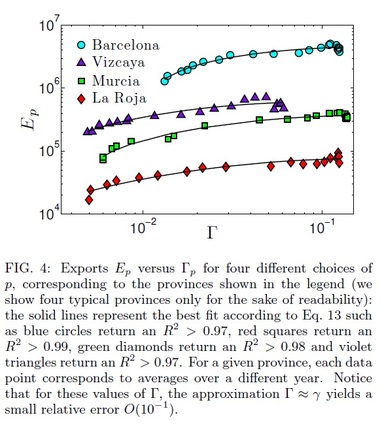
In these four plots we show the behavior of the following quantifiers versus the percentage of migrants inside the host community (not versus time!).
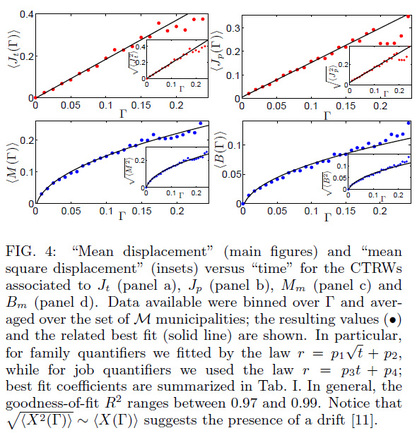
The two quantifiers in the first raw show a linear growth with migrant's density of the temporary and fixed job given to migrants: This behavior is well explained by a statistical mechanical theory where both imitation and competition are present at the microscopic level (in the dynamics of each single decision maker): a glassy system.
The two quantifiers in the second raw show a square-root growth with the migrant density of the mixed marriages and newborns from mixed parents: note that the square root behavior for the order parameters is typical of ferromagnetic interactions, suggesting that -in these cases- competition plays minor role, while imitation is prevailing at the microscopic scale.
The two quantifiers in the first raw show a linear growth with migrant's density of the temporary and fixed job given to migrants: This behavior is well explained by a statistical mechanical theory where both imitation and competition are present at the microscopic level (in the dynamics of each single decision maker): a glassy system.
The two quantifiers in the second raw show a square-root growth with the migrant density of the mixed marriages and newborns from mixed parents: note that the square root behavior for the order parameters is typical of ferromagnetic interactions, suggesting that -in these cases- competition plays minor role, while imitation is prevailing at the microscopic scale.
It is worth noticing that, beyond statistical mechanics coupled with graph theory, a completely different route can be paved for understanding social dynamics at the miscroscopic leve, namely by using a branch of stochastic processes known as continuous time random walks on which the following plots are due to.
|
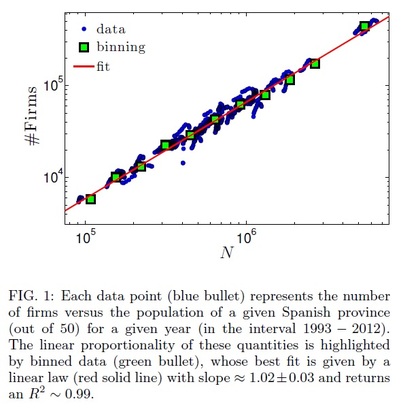
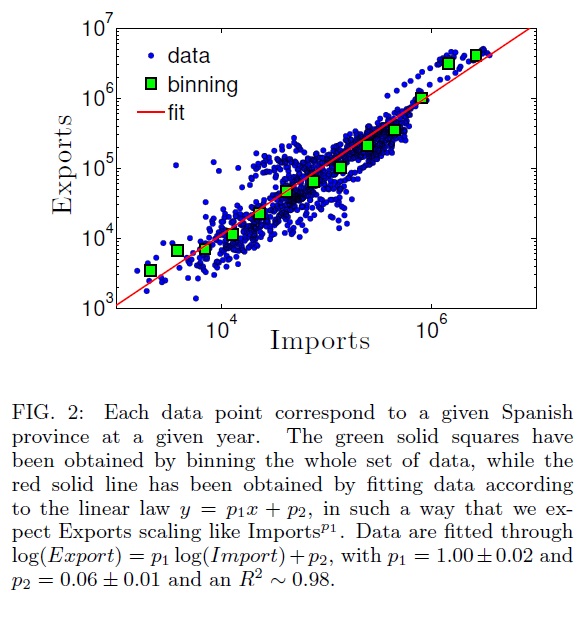
Beyond investigations on social behavior of decision makers (as shown, for instance, by analyzing the way they marry), we are interested also in economical behavior of their firms, in particular in relation with the emergent theory of Economical Complexity
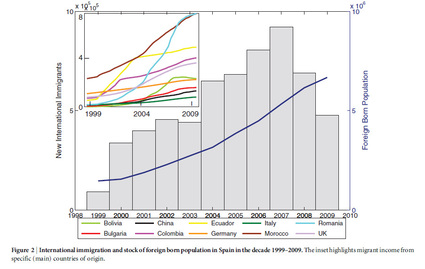
We analyse product diversification of trades for the test case of Spain and we correlate its behavior with the existence of an underlying social network of migrants interacting with natives. |
|
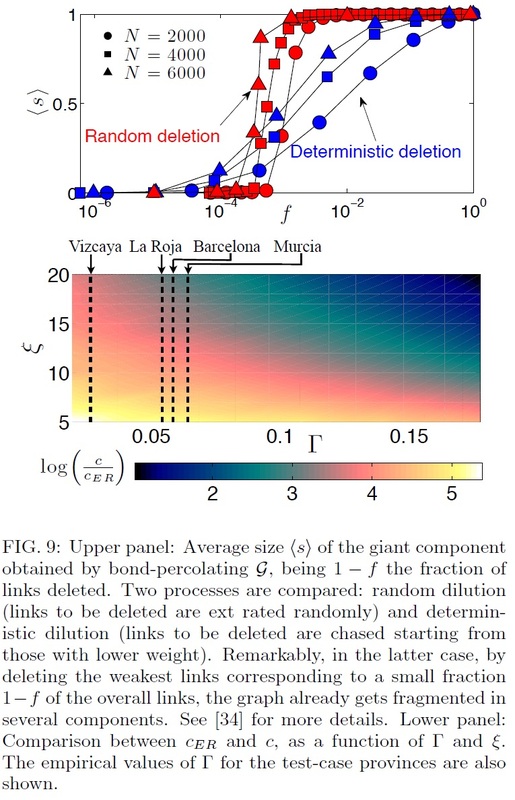
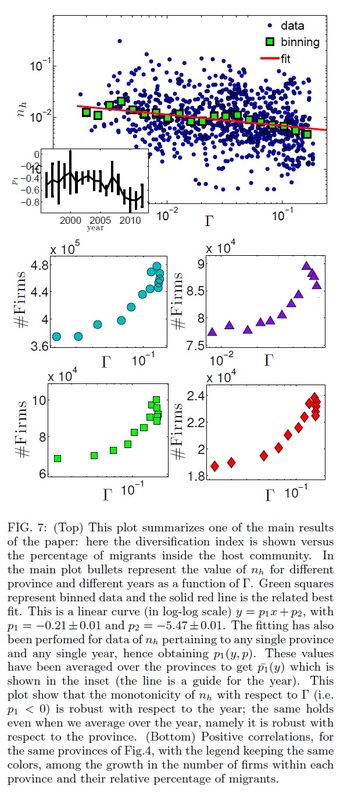
We can then contribute to the novel scenario depicted by Economical Complexity, where productions and exports for specialised countries are diversified (in contrast with classical economical predictions of specification): keeping the focus on trading (that is, exports instead of production), we prove that such a boost for diversification in the international trade market is favoured by the underlying interactions among locals and migrants. Indeed the latter, providing key information on policies and needs in their native countries, allow firm's holders to leverage transactional costs of exports and duties. As a consequence, international trading is affordable for a larger basin of firms and results in an increased number of transactions (extensive margin), which, in turn, implies a larger diversification of international traded products.
Further, as a sideline, our theory allows easily to estimate the (averaged) critical amount of migrants inside the host country before their presence starts to affect international trading and naturally implies that the social organisation of Spanish decision makers exhibits small world features. |