"White Neurons": Statistical mechanics of lymphocyte networks
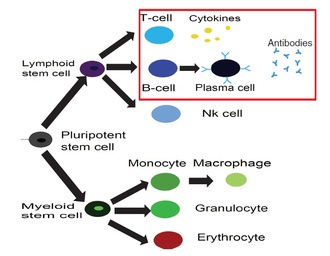
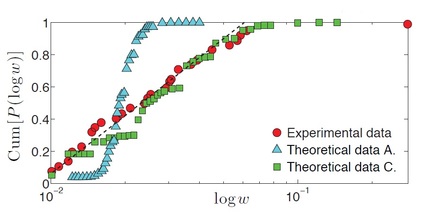
IMMUNOLOGY IN A NUTSHELL All mammals have an "innate immune response" (primary response), managed by macrophages, neutrophils, etc. (that is most basic and shared with all the other living organisms sharing an immune system) and an "adaptive immune response" (secondary response) whose main agents are lymphocytes (I will skip any detail on natural killers, as I never worked on those cells, but they are important of course!). The latter, namely the adaptive response, is particularly interesting for researchers involved in glassy physics because of its features: for instance it is able to "learn", both the molecular details of the antigen to fight (and this happens at the "local level" of a given lymhocyte, via a process known as "hypersomatic mutations"), as well as the best strategy that the lymphocyte's network as a whole has to explore in order to cope with the intruders or face malignancies, further it has both a single-agent memory and a distributed memory (the latter somehow in common with neural networks), its dynamics is metastable and spread over several timescales (with the typical fingerprint of aging), and more... Roughly speaking, these two branches of the immune system defend us both from a phetora of pathogens continuously invading our body and from deranged cells as cancerous ones, while, simultaneously, they must be aware of properly recognizing "self" (namely our cells and proteins) so to avoid killing them thus preventing autoimmune reactions. In the past four decades, giant steps have been made toward our final and systemic (that is, not purely reductionist) comprehension of the immune system, however, due to its immense complexity, a satisfactory picture of the system as a whole (able to highlight its emergent/collective properties) is still under development: our research in theoretical immunology trough "statistical mechanical glasses" aims to contribute in paving this strand. Our prime research interest in this field is understanding complexity hidden in the adaptive immune response, namely the one performed by lymphocytes (B-cells and T-cells, i.e. those enclosed in a red box in the picture above); in particular, among T-cells, we are interested in the subgroups of so-called ‘helpers’ and ‘suppressors’ (sometimes called "regulators") which form the "coordinator branch" of the immune response. We are interested also in B-cells and killer (cytotoxic) T-cells, that as a whole form the "effector branch" (coupled with further agents as Natural Killers etc.): while the former are meant to orchestrate the immune army, the latter are the real "soldiers" that physically kill or inhibit pathogens in turn present in our body. At a first approximation, to make clearness in this ensemble of different weapons and soldiers, both T cells and B cells have receptors on their external membranes (they perform pattern recognition to identify the various peptides they encounter), respectively the TCR (T-cell receptor) and BCR (B-cell receptor), which are able to bind to antigens (suitably presented to them, e.g. via the MHC complexes on their membranes by antigen presenting cells) and all the cells with the same BCRs or TCRs (depending if we speak of B or T cells) belong to the same clone. Hence if T-cells, say, A and B (and only A and B) share the the same TCR against, say, EBV, then A and B form the clone against EBV (note that the size of the clone is not constant in time: if EBV enters the body, once A and/or B will meet it, they will undergo clonal expansion that means -in these regards- duplication). In particular BCR are soluble immunoglobulins (i.e. antibodies): indeed B-cells produce antibodies which are protein (nothing but collections of BCRs dense on their cell membranes) able to recognize and bind pathogens and, as we saw, those cells that produce the same type of antibody are said to form a clone. The human immune repertoire consists of O(10^8 − 10^9) different clones over a total of O(10^11 - 10^12) cells. The size of a B-clone, i.e. the number of identical B-cells (sharing the same BCR, thus producing the same antibodies), may vary strongly (preventing standard probabilstic approaches -tacitely assuming central limit theorem convergence- to hold straighforwardly): indeed a clone at rest may contain some O(10^3 − 10^4) cells, but when it undergoes clonal expansion, its size may increase by several orders of magnitude, up to O(10^7 − 10^8) and the overall distribution of clonal sizes may become multimodal. Beyond those values of concentration, if further expanding some clones, the state of the immune system would be pathological, and undergoes a syndrome which is referred to as lymphocytosis where mistakes happen and usually autoimmune manifestations become frequent: part of our work elucidated the key mechanisms linking autoimmunity and lymphocitosis (see for instance here). When an antigen enters the body, several antibodies produced by different clones may be able to bind to it, making it chemically inert and biologically inoffensive (and more visible to other actors, as macrophages, for its removal). In this case, conditional on authorization by T-helpers (mediated via cytokines), the binding clones undergo clonal expansion and start releasing high quantities of soluble antibodies that explore the blood flow to search for and inhibit the enemy. After the antigen has been deleted, B-cells are instructed by T-suppressors, again via cytokines (this time carrying suppressive and not stimulating messages), to stop producing antibodies and undergo apoptosis (note that, even in absence of T-instructions, the lack of primarily signal -the antigen- would still work toward quiescence). In this way the clones reduce their sizes, and order is restored. This is the so called "Clonal Selection Theory" pioneering developed by Burnet (Nobel Prize for Medicine in 1960) and has been formalized in a statistical mechanical theory by us in a series of papers (see e.g. paper1 paper2 paper3). Crucially, two signals are required (within a small temporal interval) for B-cells to start clonal expansion: the first is binding to antigen (namely the presence of an infection or of a deranged -cancerous- cell), the second is a ‘consensus’ signal, in the form of an eliciting cytokine secreted by an activated T-helpers (which, in turn, must have its TCR triggered enough by some involved antigen presenting cell). This costimulation-mechanism, known as the ‘two-signal model’, prevents abnormal reactions, such as autoimmune manifestations and is at the core of self/non-self discrimination, namely the highly not-trivial capability of the system as a whole to distinguish among what is "self" (and must not be attacked) and what is "non-self" (which must be eliminated from the host body). It is worth stressing that self-directed B cells are (partially) deleted at ontogenesis trough a process called "clonal deletion" (a central tolerance mechanism); however, as always in biology, this mechanism does not work perfectly (and, indeed, it is not the solely to take care of this crucial property of the immune system) and a little amount of self-directed B cells are (on average) allow to freely circulate into the host body (hence they largely meet their corresponding "antigen" that feels their BCR): it is the lacking of the second signal -the consensus to attack by helpers- that prevents them from attacking self-cells (peripheral tolerance mechanism)! Let us focus only on B and T clones for simplicity. As we saw T helpers dialogue with B cells trough eliciting cytokines: those are stimulating signals, that can be seen as "positive links" among a T node and a B one in the bipartite graph whose parties are respectively the ensemble of T clones -both helpers and suppressors- and the whole B repertoire (see the figure at the beginning of the right column). Suppressor T-cells, instead, instruct B cells trough suppressive cytokines (inhibiting signals, that is "negative links" among a T node and a B one in the same bipartite structure as before). In the language of disordered statistical mechanics we deal with a bipartite spin-glass. Further, as each clone T interacts with only a tiny fraction of the B-repertoire, namely only with those B-cells with a pertaining BCR, this bipartite structure is hyperdiluted (stricktly speaking it displays a "finite connectivity" regime, where no giant component emerges): remarkably, in this paper, we have shown that an hyper-diluted bipartite spin-glass performs as an extensive parallel processor able to cope with several antigens simultaneously: we are hence interested in asking questions as how many megaflops of information can the immune system scan each minute? Where is the memory of the system allocated? How does information compression work in these networks? And so on... Beyond interactions among T and B clones, B cells interact even among themselves (see the picture at the top of the right column): the idea of an internal network for the B-repertoire appeared early in immunology, when Jerne (Nobel prize for Medicine in 1984) -in the 70’s- suggested that each antibody must have several idiotopes which are detected by other antibodies. Via this mechanism, an effective network of interacting antibodies is formed, in which antibodies not only detect antigens, but also function as individual internal images of certain antigens and are themselves being detected and acted upon. These network interactions provide a "dynamical memory" of the immune system, by keeping the concentrations of antibodies (especially those representing encountered antigens) at appropriate levels. Roughly speaking, this can be understood as follows: At a given time a virus is introduced in the body and starts replication. As a consequence, at high enough concentration, it is found by the proper B-lymphocyte counterpart: let us consider, for simplicity, a virus as a string of information (i.e. 1001001). The complementary B-cell producing the antibody Ig1, which can be thought of as the string 0110110 (the dichotomy of a binary alphabet in strings mirrors the one of the electromagnetic field governing chemical bonds), then will start a clonal expansion and will release high levels of Ig1. As a consequence, after a while, another B-cell will meet 0110110 and, as this string never (macroscopically) existed before, attacks it by releasing the complementary string 1001001, that, actually, is a "copy" (internal image) of the original virus but with no DNA or RNA charge inside. The interplay among these keeps memory of the past infection. However, in the 90’s, the network theory was considered to be strongly marginal: It did not appear as a part of a whole although it gave an appealing mechanism for the implementation of memory in the immune system (this may be partially due to a historical/social lack of interest for those experiments: focusing on signal transduction was unvailing enormous information -all local, hence easy to believe- on the way cells interact and interest for that analysis prevailed. Furthermore, our understanding of graph theory was very rudimental and the tacitely idea when thinking at a graph was at an overpercolated network, which was too far from immune scenarios). Recently, thanks to a much more mature perspective on graph theory, in this paper, we finally found a concrete role for the idiotypic network in accomplishing systemic anergy directly within the two signal model. The idea in a nutshell is that the idiotypic network should not be seen any longer as a "standard network" (that is, with a giant component), rather it is a strongly underpercolated network made by several disjoint "cliques": the latter however still play a (hidden and complex) role in silencing self-directed aggressions. Beyond covering a statistical mechanical formulation of these general themes, our work in theoretical immunology aims to find answers to questions as (I give hereafter just a few examples): -how many calculations is the immune system able to perform simultaneously (i.e. in terms of megaflops)? -which are the circuital equivalent processing units (as flip-flops, operational amplifiers and inverters in electronics) involved in computation behind the immune system and how do they spontaneously work? (see the biological cybernetics section too) -how is the memory of the past infection stored in the system and is the latter statical or dynamical? And if it is dynamical (as there are both statics and dynamics features in the real system), on how many timescales the phenomenon of vaccination is split? (see the neural networks section too) -how does the self/non-self discrimination work on the system as a whole? and, at least for anergy, is this a really emergent property of the whole system? -how many subnetworks build the overall system and how do they interface? -can we instruct the immune system to learn (e.g. to attack antigens -as cancer- that elude immunosurveillance)? and in which way (the strand paved by monoclonal antibodies)? (see the mathematical virology section too) -can we reset the immunological memory and/or can we be able to "rejuvenate" the systeum and bring it back at the beginning of its raise (thus strongly enhancing its capabilities)? To conclude with something more "concrete", hereafter I show a comparison among experiments on mice and our theory on systemic anergy (under the assumption of over-percolated immune networks [data A] and for highly diluted idiotypic structures [data C]). In particular the cumulative of the distribution of the logarithm of the weighted connectivity of the BB network is shown: As it is clear even by direct inspection, a giant component would result in a behavior not-in-agreement with the real one. At contrary, dealing with under-percolated network results in a nice fitting among theory and experiments. In what follows I present (mainly from a graphical perspective for the sake of simplicity) the novel experiments we are performing with LabOnChip technology. These are the result of a collaboration of our group (@Physics Department of Sapienza) with Istituto Superiore di Sanità (handling the cells) and with Istituto Nazionale di Nanofotonica (where the chip is concretely developed trough lithography): these experiments are meant to unveil the complexity of immune dialogos trough a systemic perspective that is partially missing in the present Literature. Some results have been already published (see the work 62 on my publication list) |
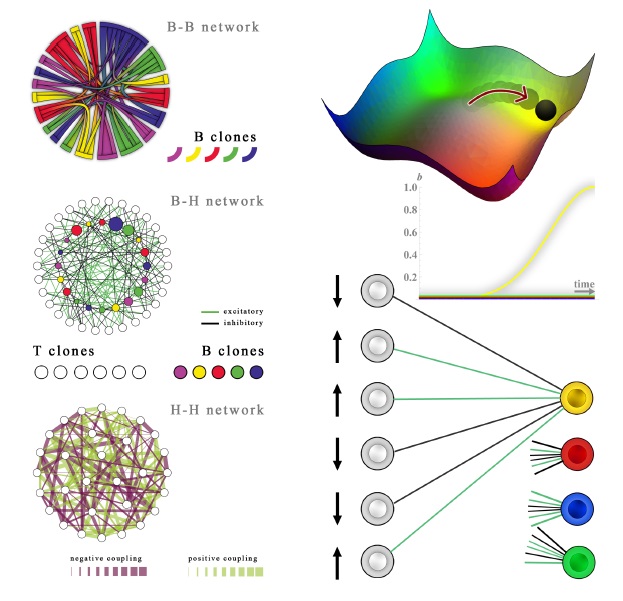
NETWORKS IN THE IMMUNE SYSTEM In the left column of the picture above, three networks are shown: The upper network is the so called idiotypic network (see left part of this page for details), whose nodes are B-clones and links mirror the reciprocal binding strenght among the corresponding BCRs of different clones. The larger the links, the stronger the interaction among their nodes (i.e. their corresponding B-clones).
The network in the middle is a bipartite network, where one party is built by B-clone (inner circle) and another party (outter circle) is made of by helper and suppressor T-clones (the bipartite spin-glass discussed in the left column of this page under the assumption of full connectivity). T-helpers and T-suppressors dialogue with B-clones via cytokines, that are small signalling proteins conveying both eliciting (exciting) and inhibiting (suppressive) stimuli, thus, in the language of statistical mechanics we speak of a bipartite spin-glass. The last network, is a network where T-clones are effectively linked alone and their dialogues are of Hebbian form, that is, they are able to spontaneously coordinate and give instructions (i.e. "expand" or "attack") to B-clones that play as soldiers against antigenic enemies. Trough statistical mechanics it is possible to show that the bipartite network where B and T cells dialogue (that is the "real" network seen under the microscope) is equivalent (it shares the same partition function) with the last network, where T-clones play as a whole in the form of a huge associative network. Their minima (shown in the second column, top right) correspond to key instructions to B-clones: once the external antigen triggers a response, helpers and suppressors candidate their best-matching B-clone to expand collapsing their free energy into the pertinent valley (yellow in the picture, as it is the B-clone expanding). In the bottom-right image we show the bipartite network during the retrieval of the yellow B-clone. Black links mirror inhibiting cytokine while green links play for stimulating cytokines. A retrieval condition implies all the T-clones connected to the yellow B-clone with black links to be quiescent (spin down), while all the T-clones connectet to the yellow B-clone with gree links to be firing (spin up), that is, effectively secreting those cytokines. This situation corresponds both to the maximum signal to expand conferred to the Yellow clone (and recovers from a statistical mechanics perspective Burnet theory for Clonal Expansion), and to the most probable thermodynamic equilibrium of the system. 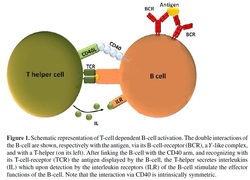
The two-signal model:
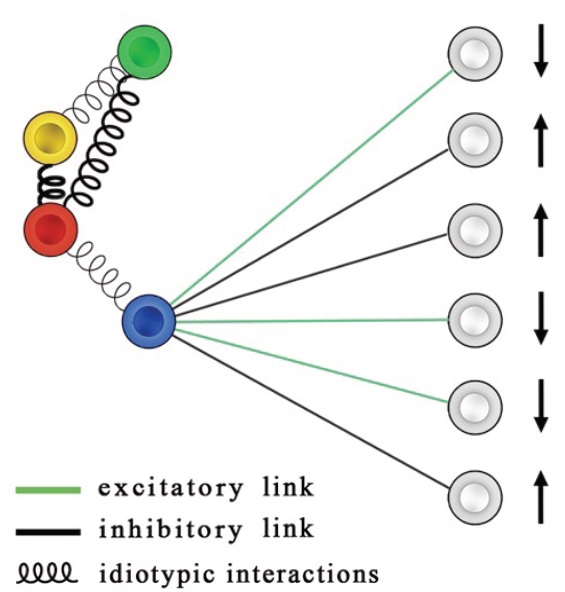
the main paradigm in modern Immunology for explaining the clonal expansion is that a given cell (a B cell in the picture) needs two signals on its membrane to get active. The first is the presence of the antigen and the secon is the presence of a "consensus", namely a cytokine secreted by a T-helper which is coupled to the B cell. From an information theory perspective, this is a marvelous stochastic AND gate. See the section Biological Cybernetics for more info on this route. MAKING THE TWO-SIGNAL-MODEL AND THE IDIOTYPIC NETWORK INTERACT This picture shows a sketch of the interplay among both the BB (idiotypic) network and the BT (bipartite hyperdiluted spin-glass) network: In particular, signals from T-clones are shown for the blue B-clone only (gree links carry eliciting cytokines, while black links account for suppressive ones).
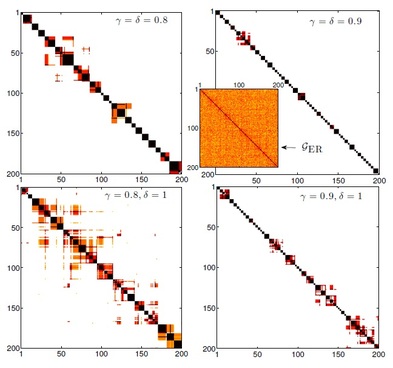
Idiotypic interactions are represented by springs, such that the higher the connectivity among two B-clones, the stronger the spring linking their nodes (for instance the spring among red and yellow clones is far from tiny, while the one connecting the red one with the blue one is tiny). As a consequence, if the blue B-clone is forced to expand by T-cells, it will be able to do that thus recovering, via statistical mechanics (coupled to graph theory), the Burnet Clonal Selection Theory as a natural outcome of lymphocyte interactions. Exampels of overlap matrix. The nodes are ordered such that nodes with large overlaps are adjacent, and the most significant part of T is around the diagonal. Note: T_ii = 1 for all i, by construction. Darker colours correspond to larger entries, and any extended coloured zone denotes a module, i.e. a set of nodes that are highly clustered and possibly not connected with the remaining nodes.
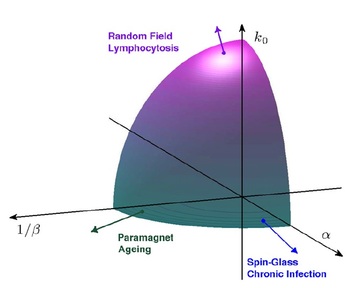
These plots refer to numerically generated graphs with 104 T-clones, ratio among T and B clones α = 0.1 (T clones are ten times more than B ones) and connectivity c = 1. To avoid cluttering of the figures, only a fraction 200 × 200 of each pattern is shown. A similar fraction of the overlap matrix for an extremely diluted Erdös-Rènyi graph made of 104 nodes is also depicted for comparison (inset). In this case there is no evidence of modularity; T displays a homogeneous pattern. PHASE DIAGRAM FOR THE IMMUNE SYSTEM. In this last plot hereafter (showing only a subset of the tunable parameters, the main ones) the coloured region represents allowed values for the parameters that let the system behave as an "immune system" (namely within this region the system displays as emergent features: self/non-self discrimination, anergic self-directed B-cells, low dose tolerance before clonal explansion, bell shaped response when attacking enemies, both static and dynamic storage of memory of previously encountered antigens, etc.). From this region three ways to escape are shown: on the alpha degree of freedom (where alpha plays for the ratio among B and T cells, that is alpha=B/T), if alpha>1 (namely if B cells are more than T cells) the system undergoes a phase transition toward a pure spin-glass phase where retrieval and coordination are no longer possible. On the noise degree of freedom (1/beta, where beta is the noise level) the system may escape the good region due to the presence of too much fast noise (which mirrors "dust in the geat" phenomena) and the system behaves as a paramagnet, while on the k0 degree of freedom, where k0 represents the amount of expanding cells, the system may escape from proper functioning becoming a random-field Ising model (whose retrieval or coordination capabilitites are again lost) and this represents the typical case of chronic infections whose most remarkable examples are HIV or EBV pathologies.
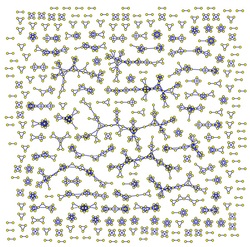
This is an example of a (part of) the lymphocyte network, whose yellow nodes account for T-clones and its blue ones represent B-clones.
As an already direct visualization may highlight the graph is highly under-percolated, with several cliques performing almost autonomously: a huge difference with respect to the neural counterpart is indeed network's connectivity. While in neural networks each neuron (both biological neurons and electronic ones) exchanges information with several other neurons [O(10^5)], in the immune counterpart -due both to the high selectivity of the B and T cell receptors and to the fact that links in this context are dynamical and played by diffusive cytokines (thus small ranged)- lymphocyte's connectivity is strongly reduced such that -on average- each lymphocyte dialogues with a finite number of partners even in the thermodynamic limit. This clearly splits the network into several disconnected and small-world clusters, each of which behaves as a small associative network, able to store and retrieve information. As we have shown here, the price to pay for these multitasking features is however that the amount of storable information is much less than that in the brain: indeed cytokines carry messages whose information content is very poor as roughly the message that T-cells pass on B-cell is "stay" or "attack", quite far from the complexity of brain thinking. 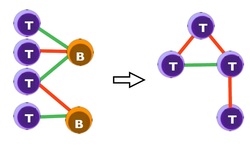
Lastly, we show an example of a "clique": in the left cluster a small, autonomous, piece of the lymphocyte network is shown: four different T-clones instruct two different B-clones (red links are inhibiting and red links are excitatory). This is what is commonly seen under the microscope. However addressing the computational capabilities of such a clique "from a direct approach" is very puzzling. We have shown that the thermodynamical (i.e. average) behavior of this small processor (able to handle and store only a few bits, but remember that there are millions of billions of these cliques in our body) is the same of the one shown on the right, where T-clones only are present and loops do appear. While not evident here, however, understanding the behavior of the right-circuit is much more easy and in particular we have shown that the bipartite structure on the left behaves as an associative network -the clique on the right- thus is able to perform learning, information processing and information storage (not the standard one of neural networks because these cliques break ergodicity only weakly, while a full symmetry breaking is required for static memories to be mantained).
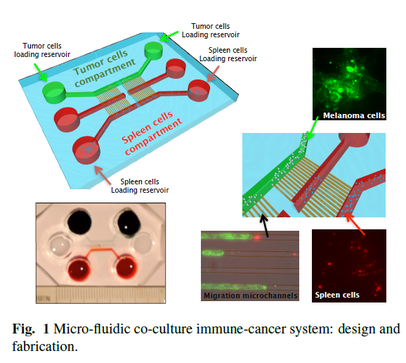
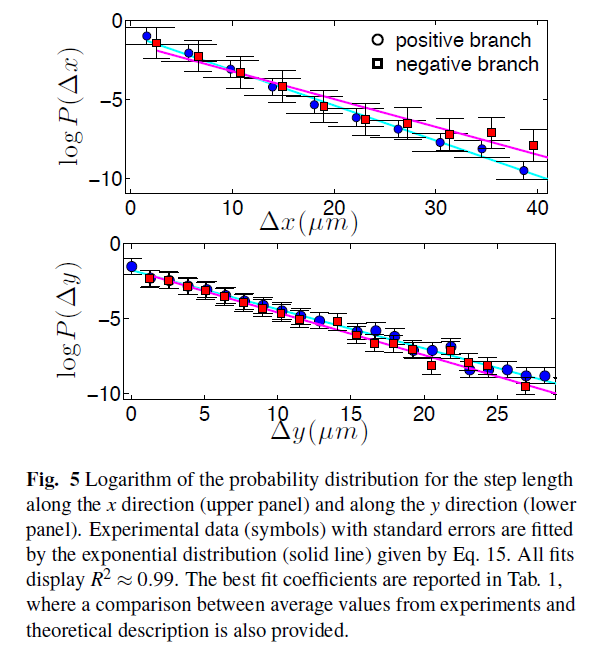
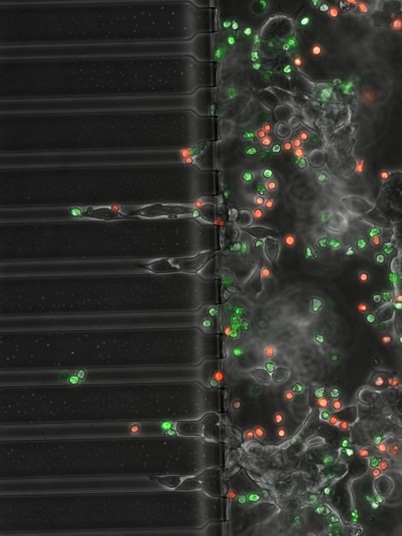
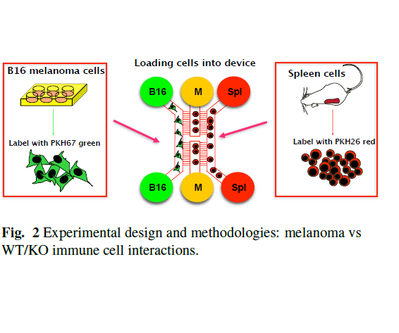
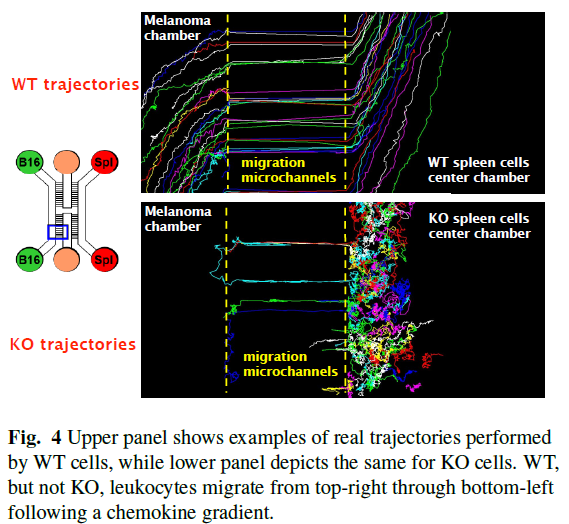
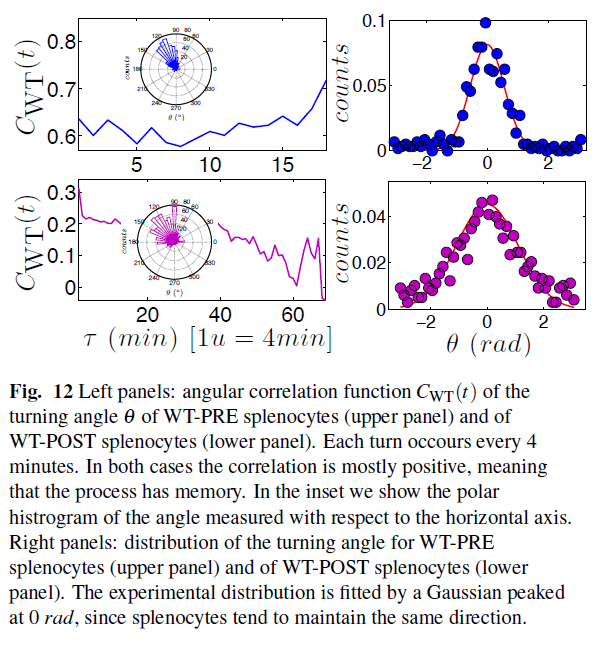
Example of patterns of migration of T cells (red bubbles) and B cells (green bubbles) attacking cancerous cells (B-12 melanoma) taken from LabOnChip experiment (further information in paper 62 in my publication list)
|